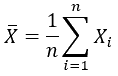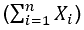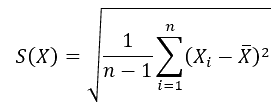التحليل الوصفي للبيانات

３- التحليل الوصفي للبيانات (LARSON و FARBER، 2012)

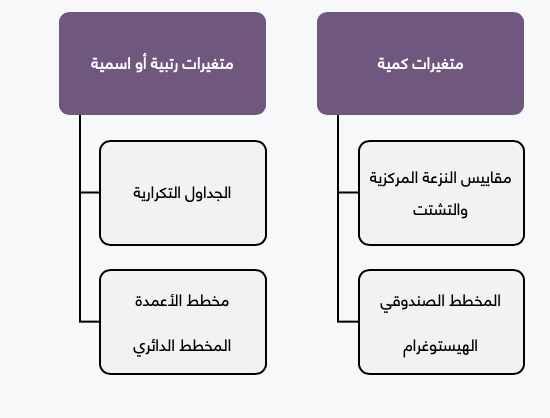
يقصد بالإحصاء الوصفي إعطاء لمحة سريعة عن البيانات باستخدام الجداول التكرارية والمقاييس الإحصائية والمخططات البيانية، وتختلف الأدوات التي نستخدمها في وصف البيانات وفقا لطبيعة المتحول:

فإذا كان اسمياً (Nominal) مثل الجنس، أو رتبياً (Ordinal) كدرجة التخرج. نستخدم عادة الجداول التكرارية (Frequency tables)، ومن المخططات نستخدم إما مخطط الأعمدة Bar Chart أو المخطط الدائري Pie Chart.
أما إذا كان رقمياً (كمياً Scale) نستخدم عادة مقاييس النزعة المركزية والتشتت، ومن المخططات نستخدم مخطط الهيستوغرام Histogram أو المخطط الصندوقي Boxplot.

وصف المتغيرات الاسمية:

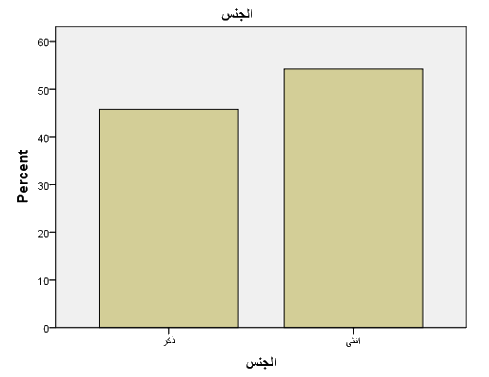
نصف المتغيرات النوعية (الاسمية والرتبية) من خلال الجداول التكرارية ومخططات الأعمدة والمخطط الدائري. يصف الجدول التكراري الآتي لمتغير الجنس كمثال عن استخدام الجداول التكرارية لوصف المتغيرات الاسمية:

الجنس


	Frequency	Percent	Valid Percent	Cumulative Percent
valid ذكر	27	45.8	45.8	45.8
valid انثى	32	54.2	54.2	54.2
Total	59	100.0	100.0	100.0

يوضح العمود الأول التكرارات (Frequency) والعمود الثاني النسبة المئوية لكل تكرار Percent فمثلا: 45.8 = 27/59×100 . نلاحظ وجود عمود آخر وهو النسبة الفعلية (Valid Percent) وهي هنا تتساوى مع النسبة العادية بسبب عدم وجود قيم مفقودة, سيتم توضيح هذا البند في الجدول 4 المقبل.

الجدول 4

الدخل الشهري


	Frequency	Percent	Valid Percent	Cumulative Percent
valid لايوجد دخل	30	50.8	51.7	51.7
valid أقل من 15 ألف	7	11.9	12.1	63.8
valid بين ال 15 و ال25	11	18.6	19.0	82.8
valid بين ال25 و ال 35	4	6.8	6.9	89.7
valid أكثر من 35	6	10.2	10.3	100.0
Total	58	98.3	100.0
Missing System	1	1.7
Total	59	100.0

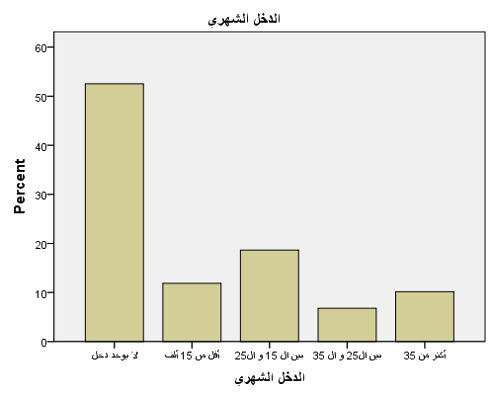
نلاحظ وجود سطر إضافي في الجدول 4 لم يكن موجودا في الجدول 3 وهو بند القيمة المفقودة (Missing) , ويتضح هنا الفرق بين العمودين (Percent, Valid Percent) فالقيمة الأولى مثلا في العمود Percent حسبت بالشكل: 30/59×100=50.8, أي آخذين بعين الاعتبار حجم البيانات الفعلية إضافة إلى المفقودة, في حين أن القيمة المقابلة لها في العمود Valid Percent فحسبت بالشكل: 30/58×100=51.7, أي تم هنا استبعاد القيمة المفقودة من حجم البيانات ليصبح حجمها الفعلي 58 فقط. وفي المخططات البيانات الآتية (الشكل 11) سيتم الاعتماد على البيانات الفعلية (valid) فقط.

الشكل 11 - أ

الشكل 11 - ب

وصف البيانات الرقمية:

تستخدم مع البيانات الكمية مقاييس النزعة المركزية والتشتت والتوزيع مع البيانات الكمية، ومن المخططات نستخدم الهيستوغرام, مخطط الساق والورقة, والمخطط الصندوقي.

تصنف لديك المقاييس الإحصائية في أربعة مجموعات مختلفة، وهي:

مقاييس النزعة المركزية Central Tendency وتفيد في وصف مكان تمركز البيانات، المقاييس التي سنختارها هنا هي:
- المتوسط Mean , ويعطى بالصيغة:
- الوسط Median (الوسيط) وهو القيمة التي في المنتصف بعد ترتيب القيم تصاعديا أو تنازليا.
- المنوال Mode: وهو القيمة الأكثر تكرارا.
- مجموع البيانات Sum
مقاييس التشتت Dispersion وهي المقاييس التي تصف تشتت البيانات عن المتوسط، وسنختار منها:
- الانحراف المعياري Standard Deviation: ويعطى بالصيغة:
- أكبر قيمة Maximum
- أصغر قيمة Minimum
- المدى Range وهو الفرق بين أكبر قيمة وأصغر قيمة
مقاييس التوزيع Distribution: وهي تصف شكل توزع البيانات، كالتناظر والتفلطح.
قيم المئين Percentiles: وهي تصف تشتت البيانات عن الوسط (الوسيط).

يوضح الجدول الآتي مقاييس إحصائية مختارة لمتغير العمر الرقمي:

تفسير المخرجات:

يتضح أن حجم البيانات الإجمالي هو 59 فردا, منهم 56 فردا أجابوا عن سؤال العمر (بيانات صالحة Valid), و 3 أفراد لم يجيبوا عن سؤال العمر (بيانات مفقودة Missing).
بلغ متوسط أعمار زبائن صالة ريبون هو 25.96 أو 26 سنة وبانحراف معياري 7.8 سنة, مما يعني أن زبائن الصالة هي من شريحة الشباب.
في حين بلغت قيمة الوسط 23.5 , وتراوحت 50% من أعمار الزبائن بين 21 سنة و29 سنة. والذين يمكن وصفهم بأنهم الشباب حديثو التخرج من الجامعة. ومن الواضح أن الوسط أصغر من المتوسط, مما يدل على وجود عدد لا بأس به من الزبائن المتقدمين بالسن (أو المخضرمين) قد رفعوا من قيمة المتوسط كون المتوسط يتأثر بالقيمة الشاذة.
أقل الزبائن عمرا هو 11 سنة, وأكبرهم عمرا هو 50 سنة (ومدى الأعمار هو 39 سنة)

يوضح الشكل الآتي مخطط الهيستوغرام:

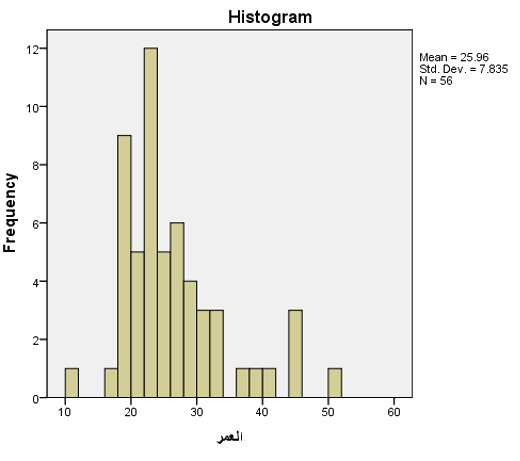
يوضح المخطط أن غالبية البيانات تتوزع حول الفئة العمرية 20-30 سنة , مع وجود بسيط لبعض الأفراد اللذين أعمارهم بالأربعينات والخمسينات.

اختبر نفسك:

من مقاييس النزعة المركزية: ( يمكن اختيار أكثر من إجابة )
- المتوسط الحسابي.
- الوسيط.
- المنوال.
- المدى.
من مقاييس التشتت : ( يمكن اختيار أكثر من إجابة )
- الانحراف المعياري.
- المدى.
- الوسيط.
- التباين.
تضم الجداول التكرارية :
- تكرارت قيم المتغيرات فقط.
- النسب المئوية لقيم المتغيرات فقط.
- معرفة توزع بيانات كل متغير حول متوسطه.