قوانين شائعة لتقدير حجم العينة
1. يعطى حجم العينة وفقا لقانون توماس ثيمسون بالعلاقة (د. أبو شعر، 1997):
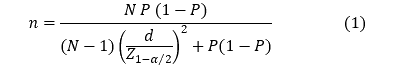
حيث أن:
- n حجم العينة.
- N حجم المجتمع.
- d حد الخطأ المسموح به.
 القيمة الحرجة للتوزيع الطبيعي المعياري عند مستوى دلالة
القيمة الحرجة للتوزيع الطبيعي المعياري عند مستوى دلالة  .
.- P احتمال تحقق الصفة المدروسة في المجتمع.
وعندما تكون P مجهولة يفضّل ثيمبسون أن تؤخذ: P=0.5
يستخدم هذا القانون عندما يكون حجم المجتمع محدودا, لكن عندما يكون حجم المجتمع كبيرا جدا, فإن قانون ثيمبسون (1) يصبح بالشكل:
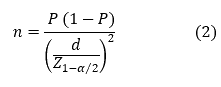
كما يعطى حجم العينة لمجتمع غير محدود بصيغة أخرى شبيهة وهي (Cooper و Schindler، 2008):
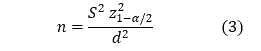
وهي صيغة حساب حجم العينة في حال كون المجتمع كبيراً بما فيه الكفاية. حيث أن:
-
 هو تباين المجتمع
هو تباين المجتمع - d هو الخطأ المسموح به من الناحية التطبيقية
 هي القيمة الحرجة للتوزيع الطبيعي، فإذا كان مستوى الدقة المطلوب هو 95% فإن قيمته تصبح
هي القيمة الحرجة للتوزيع الطبيعي، فإذا كان مستوى الدقة المطلوب هو 95% فإن قيمته تصبح
نحن بالطبع لا نعلم تباين المجتمع 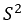 وتباين متوسط العينة
وتباين متوسط العينة 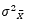 , لكننا نستطيع إيجاد القيمة التقديرية له من خلال إحدى الطريقتين:
, لكننا نستطيع إيجاد القيمة التقديرية له من خلال إحدى الطريقتين:
![]() يمكن تحديد قيمة تقريبية لتباين المجتمع
يمكن تحديد قيمة تقريبية لتباين المجتمع 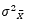 من خلال :
من خلال :
- دراسات سابقة حول نفس موضوع البحث
- عينة تجريبية من المجتمع (Pilot Study) بحيث نجري الدراسة المطلوبة على عينة حجمها
وبناء على قانون توماس سيمبسون، فإن حجم العينة للمجتمعات المحدودة يكفي أن يتجاوز 384 (إذا افترضنا أن P=0.5) أو يتجاوز 322 (إذا افترضنا P=0.33) عند سوية ثقة 95% وبهامش خطأ لا يتجاوز 5%.
ومع انخفاض هامش الخطأ المسموح به يزداد حجم العينة، وينقص حجم العينة مع ازدياد هامش الخطأ المسموح به.
كبيرا كفاية مثل 30, ونعتبر تباين هذه العينة هو تقدير لتباين المجتمع نستطيع من خلالها وضع قيمة تقريبية لتباين المجتمع.
![]() طريقة سدس المدى، بمعنى يتم وضع الحد الأقصى المتوقع للفرق بين أكبر قيمة وأصغر قيمة ممكنة في المجتمع، ثم تقسيم هذا المدى على 6 واعتباره تقريبا مقبولا للانحراف المعياري للمجتمع.
طريقة سدس المدى، بمعنى يتم وضع الحد الأقصى المتوقع للفرق بين أكبر قيمة وأصغر قيمة ممكنة في المجتمع، ثم تقسيم هذا المدى على 6 واعتباره تقريبا مقبولا للانحراف المعياري للمجتمع.
مثال: إذا كنا نهتم بتقدير متوسط أعمار مجتمع ما بالسنوات. فإنّنا قد لا نهتم بوجود خطأ في التقدير بما لا يتجاوز الشهر، يكون بذلك الخطأ المسموح به هو 1/12. وبفرض أنّنا نريد سوية الثقة أن تكون 95%, فإنّ: 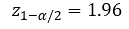 ومنه فإنّ:
ومنه فإنّ:
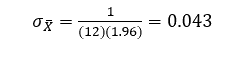
2. معادلة روبرت ماسون لتحديد حجم العينة:وهي تكافئ معادلة توماس ثيمسون ولها الشكل التالي:
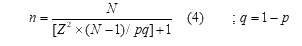
3. معادلة ريتشارد جيجر[]:تستخدم هذه المعادلة في حالة المجتمعات المحدودة وغير المحدودة
![]() حجم العينة محدود تأخذ المعادلة الشكل التالي:
حجم العينة محدود تأخذ المعادلة الشكل التالي:
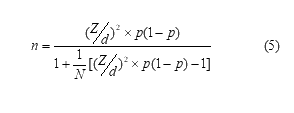
![]() حجم العينة غير محدود يحسب حجم العينة بالشكل التالي:
حجم العينة غير محدود يحسب حجم العينة بالشكل التالي:
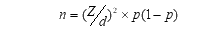
إنّ معادلة ريتشارد جيجر هي المعادلة المتعمدة لحساب حجم العينة في الدراسات التي تجريها المؤسسات التابعة للأمم المتحدة(مثلاً: منظمة الأوتشا في برنامج NPM ).
من خلال موقع The Survey System
وموقع Survey Monkey

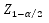 القيمة الحرجة للتوزيع الطبيعي المعياري عند مستوى دلالة
القيمة الحرجة للتوزيع الطبيعي المعياري عند مستوى دلالة 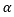 .
.